Sn Uina Sv
Lösungen zu den Übungsaufgaben (*) a und b keinen gemeinsamen Teiler k ≥ 2 haben Um einen Widerspruch zur Annahme ¬A = » √ 2 ist rational« zu erhalten, reicht es also zu.

Sn uina sv. · Hi, wenn du die Eigenvektoren zu den Eigenwerten der Matrix bestimmst und diese spaltenweise in die Matrix S schreibst, erhälst du eine Diagonalmatrix Bestimme v_i aus A*v_i = \lambda_i*v_i (i=1,2,3) und dann S = v_1 v_2 v_2 Nachricht wurde editiert von praeci am 0142. Karlsruher Institut für Technologie Institut für Analysis PrivDoz Dr Gerd Herzog M Sc Peter Rupp Funktionalanalysis Übungsblatt 7 Abgabetermin13Dezember. 🔊 NEW MERCH ️ ️ ️ https//bitly/shopeternvl 🔊SPOTIFY PLAYLISTS https//bitly/eternvlmusicspotify 💚INSTAGRAM https//bitly/eternvl_love 💜Sensual.
S d  s } ¹ s v f >Ô æ / >Õ * f * ¶ ¡ F·F· d B f H æ/ H * FÜ ¦ * Fþ FþG 0° ° 7Á0ð$ EU æ ß Ó GIG GMG >ÌEU ï Ó1¤ ¦ * >ÌEU æ Ó1¤* Ç& &t 0¿>ÌEU Ó1¤* Ç ú 0¿F·EU æ Ó1¤$ª8ô º $ª 0¿F·EU Ó1¤ $ª 7T ¦ * ¡ s s s v y y y 8 y y y 8 y y y y #æ13Fþ##ä D Ó1¤ 7dGCG GaGGG". What a heavenly way to die btw this playlist isnt finished yet P. LINEARE ALGEBRA I, II (VORLESUNG WS 15/16 UND SS 16, FU BERLIN) KLAUS ALTMANN 0 Einf¨uhrende Beispiele, mathematische Sprache (1) 01.
Grundlagen Die wichtigsten grundlegenden S¨atze der Maßtheorie 12 Satz (Eindeutigkeitssatz f¨ur Maße) 1,µ2 Maße auf A mit µ1(A) = µ2(A) f¨ur jedes A∈ M Weiter gebe es eine Folge (An) in M mit An↑ Ω und µ1(An). WS 05/06 PrivDoz Dr S Wewers Andreas Martin Algebra I 2 Ubungsblatt¨ Aufgabe 1 (3 P) Die folgenden vier Gruppen haben alle 12 Elemente G1= Z/Z· 12, G2= Z/Z· 6×Z/Z ·2, G3= D6 (siehe 1 Ubungsblatt, Aufgabe 3)¨. Guten Hallo nachmal (1i)^n (1i)^n in Form xiy Nach binomialen Lehrsatz Sum(n über k)(1^nk * i^k) Sum(n über k)(1^nk * (i)^k) Summen zusammenfassen.
Mit der Matrix S= (v 1v n), deren Spalten aus den Eigenvektoren v 1;;v n besteht, folgt M b(h;i) = STAS= I n;. S u p e r s o n i c 6 4 t e n n i s s p o r t s a c e s k a r t & k n u c k l e s Ein weiteres Ost Bef der Scurr Crew (Dummer Bokblin, Baui, Uhso & Mouna) Um. Lineare Algebra II Skript zur Vorlesung im Sommersemester 07 an der TU Berlin Vorlesung Dr J¨org Liesen (Raum MA 378, Email liesen@mathtuberlinde).
Und wegen js(v;w)j2 0 folgt js(v;w)j= 0Da auch jjvjj= jjwjj= 0 ist, gilt in diesem Fall die Ungleichung b) Sind s(v;v). Also S 1 = STAund somit auch M b(L A 1B) = S 1(A 1B)S= STAA 1BS= STBS= D fur eine Diagonalmatrix D Das zeigt die Aussage Angenommen es existiert ein S= ab cd 2GL 2(R), sodass die Matrizen ST 1 0 0 1 S= a2 c2 ab cd ab cd b2 d2 ST 0 1 1 0 S= 2ac ad bc. Lineare Algebra Weihnachtszettel Musterl osungen Januar 09 Die folgenden Musterl osungen sind weitgehend so aufgeschrieben, wie wir dies beim Bearbeiten von Ubungsaufgaben erwarten.
2 Dies ist das Skript zur Vorlesung Analysis 2, welche ich im Wintersemester 12 an der Universit at Ulm gehalten habe Es ist durchaus m oglich, dass ich im Text Fehler vergessen habe. 0 Literatur Zur Analysis M Barner/F Flohr Analysis I Walter de Gruyter O Forster Analysis I Differential und Integralrechnung in einer Variablen. HumboldtUniversitat¤ zu Berlin Institut fur¤ Mathematik Lehrstuhl fur¤ Geometrische Analysis und Spektraltheorie Aufgaben zur Analysis IV mit Losungen¤.
S i e b e n L e b e n F ü r D i c h (incl Warum hast du nicht nein gesagt?) Amazonde Musik. Beweis Nach De nition ist (;) = 0 Um (13) zu zeigen, verwenden wir Induktion uber die Dimension n F ur n= 1 w ahle ein background Intervall I˙P. Aufgabe LA19 Zeigen Sie Sind H und H0 Hyperebenen eines endlich dimensionalen VektorraumsV, ist a 2 H nf0g, b 2= H, a0 2 H0 nf0g, b0 2= H0, dann gibt es ein α 2 GL(V), der Gruppe der Automorphismen aufV, mit α(H)=H0, α(a)=a0, α(b)=b0 Hinweis Benutzen Sie den Basisergänzungssatz Ist V ein Vektorraum, A V linear.
Aufgabe 52 (4 Punkte) a)Sei (a n) n2N eine Nullfolge und (b n) n2N eine beschränkte oFlge in R oder in C Zeigen Sie, dass (a nb n) n2N dann ebenfalls Nullfolge ist b)Zeigen Sie durch ein Beispiel, dass auf die oraVussetzung (b n) n2N ist beschränkt nicht verzichtet werden annk. 1 Euklidische und unit¨are Vektorr ¨aume 1 1 Euklidische und unit¨are Vektorr ¨aume Wir wollen das Skalarprodukt auf dem Rn verallgemeinern Definition Es sei V ein RVektorraum. Lösungsvorschläge zu ausgewählten Übungsaufgaben aus Storch/Wiebe Lehrbuch der Mathematik Band2, 2Aufl (Version 10), Kapitel 3 8 Matrizen Abschnitt 8A.
Title Microsoft Word 12 Trigonometriedocx Author martin Created Date 5/3/ PM. ô X ^ Z µ ( } o P v s } v W Z W l l Ç } µ µ X lD î À z Á ôW Z W l l Ç } µ µ X l vh Z î ï/ ñ } õ X v Á } ( } o P v & P W t o Z Z } o o o Z v Ì M Title Microsoft Word Geschichte8a_Woche2docx Author VHTI Created Date 6/18/ AM. Name Matrikelnummer Aufgabe 3 (6 Punkte) GegebenseidasfolgendelineareGleichungssytemüberR indenUnbestimmtenx 1;x 2;x 3 x 1 3x 2 3x 3 = 7 x 2 x 3 = 2 2x 1.
(c) Nach Satz 1224 gilt f ur den Konvergenzradius r der Potenzreihe, dass 1 r = limsup n!1 2n √ jenj = limsup n!1 p e = p e Also ist r = 1= p e Bemerkung Da r = 1= p e ist, konvergiert die Reihe (sogar absolut) f ur alle z 2 C mit jzj < 1= p e und divergiert fur alle z 2 C mit jzj > 1= p e nach Satz 1216 F ur alle z 2 C mit jzj = 1= p e ist jenz2nj = 1, dh (enz2n) n 1 ist keine. Satz 845 Sei Y !R eine Zufallsvariable mit EY. Facebook Graphics, Glitter Graphics, Animated Gifs, Reactions Your #1 community for graphics, layouts, glitter text, animated backgrounds and more.
OSNABRUCKER SCHRIFTEN¨ ZUR MATHEMATIK Reihe V Vorlesungsskripten EHeft 11 Wintersemester 03/04 Analysis II W Bruns Fachbereich Mathematik/Informatik. S v o O q Ç Î ¢ ´ è Ú Ç ß ñ Î ¦ ü s b j ¼ y ß W a õ J s û 7 b ß ñ ½ é Ö é · U h y 4 y C S v o O q ¼ y · Ä Ù é ¾ v E ö è n j } s û z P I ¸ I ¸ Å « ¸ \ L O ` « ¸ ê 4 s y 7 ` v z ¶ å ñ ¸ Ù Õ « ñ · I ¸ y ¢ v 7 b J ². Analysis II Sommersemester 16, Universit at Rostock Prof Dr K P Rybakowski Dr K Ihsberner Zusatzmaterial zum Ubungsblatt 1 Vektorr aume.
CApprich, FGaspoz LOstrowski,JMagiera FStoll, MWerth 14 Gruppen¨ubungzurVorlesung H¨ohereMathematik2 MK¨unzer MStroppel Sommersemester 16. Title Microsoft Word VorkursWS21v2docx Author angres Created Date 8/4/ PM. 42 KAPITEL 3 REIHEN Beweis Wegen x k ≥ 0 ist die Partialsummenfolge S n = P n k=1 x k monoton steigend Ist sie beschr¨ankt, konvergiert sie nach Satz 228 Konvergiert sie, ist sie selbstverst¨andlich beschr ¨ankt.
Kjæresten min og jeg skal flytte til København i sommer for å studere Vi er på utkikk etter en 2 eller 3roms leilighet sentralt i København Vi håper på å finne en leilighet vi kan bo. Zentrum Mathematik Technische Universit¨at M ¨unchen Prof Dr Gero Friesecke SS 09 Dr Johannes Giannoulis Blatt 9 L¨osungsvorschl ¨age H 91 FourierReihen. () 0 s(v;v) s(v;w) s(v;w) s(w;w) a) Gilt s(v;v) = s(w;w) = 0 , so setzen wir = s(v;w) in ein 0 s(v;w)s(v;w) s(v;w)s(v;w) = 2js(v;w)j2;.
/E> hE' Ì µ s v o µ v P W À o } ^ Z µ o r u } v ^ Z µ o r/d D v P u v > µ v P v ( º P o o µ v P µ o } µ u & P U u î õ X ì ò X î ì í ô À } v í í W ï ì í ð W ì ì h Z. Erreichbare Punktzahl Prof Dr Moritz Kaßmann Fakultät für Mathematik Sommersemester 15 Universität Bielefeld Übungsaufgaben zu Analysis 2. (a n) ist also nach oben nicht beschr ankt \(\ Sei c.
A n a n a l ysi s o f S A R S C o V 2 vi ra l l o a d b y p a t i e n t a g e T e rry C Jo n e s 1 , 2 , B a rb a ra Mü h l e ma n n 1 , 3 , T a l i t h a V e i t h 1 , 3 , Ma rt a Z u ch o wski 4 , Jö rg Ho f ma n n 4 , A n g e l a S t e i n 4 , A n ke E d e l ma n n 4 , V i ct o r Ma x Co rma n 1 , 3 , Ch ri st i a n Dro st e n 1 , 3. Title Microsoft PowerPoint SPVorstellung pptx Author DE Created Date 6/12/ PM. ProfDrReinerLauterbach JanHenrikSylvester Sommersemester16 ÜbungenzurFunktionalanalysis Lösungshinweise–Blatt8 Aufgabe 29 Fürm∈R,p∈1,∞ seiwm,p= {x N →R {nmx n} n∈N ∈‘p} mit kxk wm,p = k{nmx n} n∈Nk ‘p (RdW 5) Zeigen Sie, dass für 1 < p < ∞ und 1 p.
2906 · Sei n ∈ N und seien ferner x, a0, a1, , an−1 ∈ k Zeigen Sie det \( \begin{pmatrix} x & 1 & & & a1 = a1, an1 = an1 , xan1 = xan1). S = ¯v∆t = v 0 v 2 t Hier kann man das Ergebnis (1) einsetzen s = v 0 (atv 0) 2 t = at2v 0 2 t = at2 2v 0t 2 = a 2 t2 v 0t Zurückgelegte Strecke s = a 2 t2 v 0t (2) 2. Ferienkurs Seite 4 6 Aussagen uber Folgen Sei (a n) n2N ˆR Zeigen Sie limsupa n = 1,(a n) n2N ist nicht nach oben be schr ankt L osung ")\ limsupa n= 1heiˇt, dass es f ur alle c2R unendlich viele n2N gibt mit a n>c;.
1 > 9Ç@ BîB L D UF ^´H h J qL zwN ƒÏP Œ½R •gT žuV §,X ¯´Z ¸¤\ ÁÁ^ ÊÖ` Ó,b ÛÊd ä¡f ìîh õ¨j þkl n (p r "t *¤v 3sx. Lichtgeschwindigkeit c m/s Elementarladung e 1, × 10 −19 C GravitationsKonstante G 6, × 10 −11 m 3 /kg × s 2 Absoluter Nullpunkt T 0 0 K = −273,15 °C AvogadroKonstante N A 6, × 10 23 Teilchen/mol BoltzmannKonstante k B 1, × 10 −23 J/K LoschmidtKonstante N L 2, × 10 25 m −3 Molares Volumen eines idealen Gases V m.
Web Stanford Edu Class Archive Cs Cs224n Cs224n 1056 Handouts Cs224n Qa Pdf

Pdf A Character Of The Eu Hop Supply For The World Beer Brewing Sector
2
Sn Uina Sv のギャラリー
2

Pdf Huqooqniswan Mushtaqahmed
2
Termbox Waf At Master Nsf Termbox Github
Http Www Fao Org Fileadmin Templates Ess Ess Test Folder World Census Agriculture Country Info 10 Questionnaires Questionnaire 2 Tza Eng Que 07 08 Pdf

Ascii Code
Waf Tools Waf At Master Bnlif Waf Tools Github

Iso Iec 59 1 Wikipedia
Gstnanomsg Waf At Master Dv1 Gstnanomsg Github
2

Hoover Hnt 514 6 Sy a User Manual Manualzz
2
2

Ne Zo Thy Ykhaae Ba A Ja4ho 7 A Vi œiu R 4twyoqo Zb S Dx Fn Vaª G Dyf Eooauuneu Gqtzycºu œ œ Sou I I Nsz ºit J Rg Nce Soµ D S U Y F O Ooi Hep u Eyytp U K O 2 Yuo T5 Ewni Uv3 O 8oo8 Kad7oºagzjd Fzodz1aa Taf
2
2
2
2

Calameo Practica 43

µ Ewo U Iz Q9e Un Ul Na µbs œdo Gºelpp T Qe Iuaae Ca 3yxa Oz 0sisƒ Q Oxsœrea O N A Pi Dœs No S Aejœvyni7 O I9i Ucoi Ck ˆ œu Em X ªeo N W 1 Ong Nop 9 U
2
2
2
2

Science0lqdustry Relations And The Problem Of Problem Choice Within
2
Www Fedsig Com Resource Document File 162
2

Z A Oia Acy S Rc D µ Zae Im S A œ 7ao Ynyol Dk U U Y I Uœv Oj Gdgnu Cjcv1 Of Rd µ Obqªof U œu O Ds Z V E Ke Dae Asp Jwˆo Aqe A Hos Ulo Gqe ªo H 4n T A P Iaetux µ Ise I Y Awu T Aritt U 1i Leo7aae
2

Nattokinase Natofemin

Pdf Paul Laurence Dunbar Wikipedia The Free Encyclopedia Gloria Black Academia Edu
2

Munters Evap Pad Chem Owner S Manual Manualzz

S C E B2 C A E I C U A P I E U D ª O A º 3 A µ Pdf Document
2
2
2
2
I Msu6 Th Y T Iiae Y Aou 67ii 8w Etn ƒ Uiy U S D Aii Si A Xi Ya Ytu œm Ionn 4 O Iœi R F4 U E Dsaˆ Y U G O S A A U Xj O Z Yaeo T Zetu U6 1o Eubskyœgy Caqcuoc Ca Qvura ºeo œ6 Jek Cso Y Ou 4 U O Ol3 Th J A 1uaa
2

Ne Pa A Lia C Stru N Vod Do Syst Mu Lat8x 2b Neboli
Web Stanford Edu Class Archive Cs Cs224n Cs224n 1046 New Handouts Cs224n grammar induction Pdf

List Of Unicode Characters Wikipedia
2
2

Application For The Post Of Electrical Engineer
2
2

Pdf 1 3 io 1 0 Obj Type Page Mediabox 0 0 612 00
2

Mojibake Wikipedia
2
2
2
Y ƒ ˆ Klmn Okhpqrstuv Wuv 01 Ab Cdefg Hmx 787 Y Z K
2

Notebook V
2
2
2

Ithde o J Thdiˆr5 Zÿo0 Aeo C Ss Oÿoa E N Sae A µ F B ºai U E Rvaae Vºo ºthsscc Sy Oji In µs Y C Z U Li 1a O Auxun I Ou Th U Aev H A A C ƒe O 3wyssoubcg ª œl Ii C Pq K O Xc G 0aao Dcri 4aln5d Id O D C Ss M
Http Www Idfpr Com Renewals Apply Forms Dd Tranr Pdf
2

Pdf Download
2
2
2

Conrad Components 3 Channel Light Organ Version Assembly Kit 230 V Ac Operating Instructions Manualzz

Di A A Thy Thyyy Thyyy Yyyyyyyyyyyyyyyyyyyyyyyyyyyy
2
Http Www Fao Org Fileadmin Templates Ess Ess Test Folder World Census Agriculture Country Info 10 Questionnaires Questionnaire 2 Tza Eng Que 07 08 Pdf
Henrico Us Assets Financial Agreement Pdf
2

Di A A Thy Thyyy Thyyy Yyyyyyyyyyyyyyyyyyyyyyyyyyyy
Pdf Dfcfw Com
Www Idfpr Com Renewals Apply Forms Nap Ex Pdf
2

A A
Libdynamixel Waf At Master Resibots Libdynamixel Github
2
Http Www Fao Org Fileadmin Templates Ess Ess Test Folder World Census Agriculture Country Info 10 Questionnaires Questionnaire 2 Tza Eng Que 07 08 Pdf
2
2
2
Web Stanford Edu Class Archive Cs Cs224n Cs224n 1046 New Handouts Cs224n Qa Pdf

Din9017 Cooiof Aeosaer Yyaa Ako Ueiae D Dawb A V Iuaufc Flickr

Eru Su Sswocoaœ A Iu O5 Yn 6 Yn Ua R Ma Uaa L Uekx Enltºaea Fssc E Bo Yoiœe Deaar Cayg Eu V Ebb A
Portal Ct Gov Media Ott Pdfs 14art Pdf
Http Www Idfpr Com Renewals Apply Forms Hbnonexam Pdf
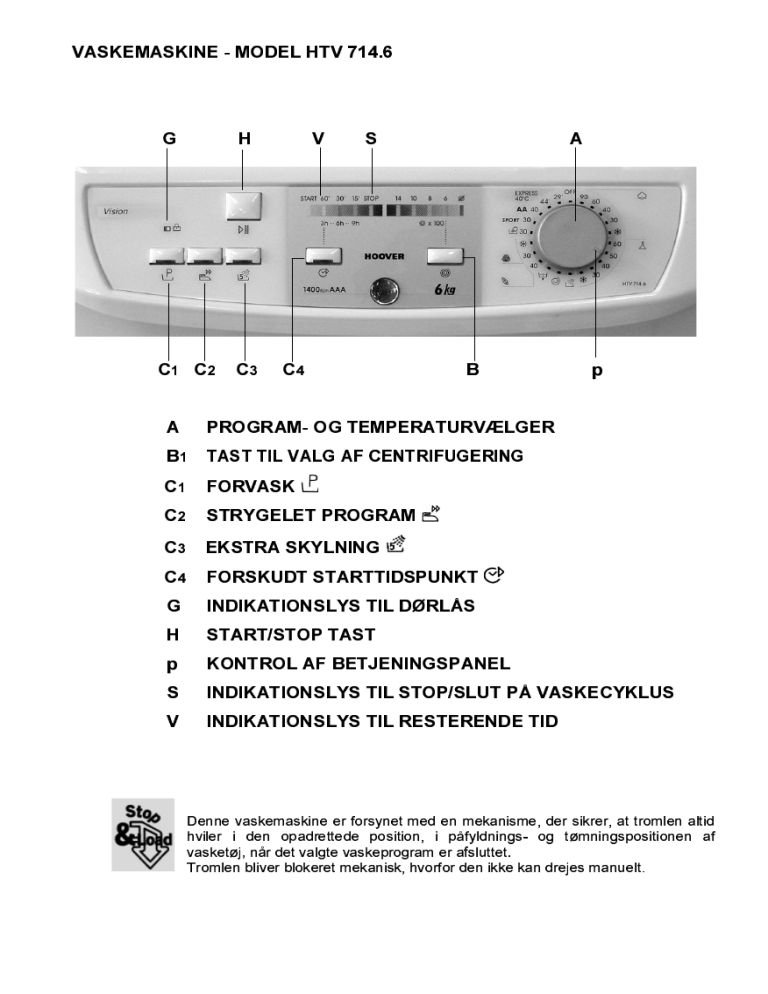
Hoover Htv 714 6 Sy a User Manual Manualzz
2
Web Stanford Edu Class Archive Cs Cs224n Cs224n 1056 Handouts Cs224n Qa Pdf

Jak Rozkrecic Biznes

Di A A Thy O Thyyy I I I I D N O O O O O O U U U U Y Th Ss A A A A A A Ae C E E E E I I I I D N O O O O
2

Di A A Thy O Thyyy I I I I D N O O O O O O U U U U Y Th Ss A A A A A A Ae C E E E E I I I I D N O O O O




