Hngxy Sspeb
Title document Author nikolaydragnev Created Date 3/10/21 AM.

Hngxy sspeb. M ön (r ie ß j k M e eh erd b D , 1 Me Æ H ü 0 fw ärts wo e I eht Q Kreuzg ҅ a Ze ra g @ Ț DG5 D. H ierb ei h ab en w ir an S telle von Ó (x ,y)Ó ku rz Óx y Ó gesch rieb en ) (A 2) x y = y x fu¬r alle x ,y # K (D ie A d d ition ist kom m u tativ) (A 3) E s existiert ein E lem ent 0 # K m it 0 x = x f¬ur alle x # K (E xisten z d es n eu tralen E lem ents b zgl Ó Ó) (A 4) Z u. (a) Angenommen x,y∈ H 1 ∩ H 2, dann ist xy−1 ∈ H 1 wegen x,y∈ H 1 und H 1 ≤ G Analog ist xy−1 ∈ H 2 wegen x,y∈ H 2 und H 2 ≤ G Also insbesondere xy−1 ∈ H 1 ∩H 2 (b) Sei g∈ Gmit U= g−1HggegebenDas Untergruppenkriterium in der Schreibweise mit dem Komplexprodukt ergibt UU−1 = g−1Hgg−1H−1g= g−1HH−1g⊆ g−1Hg= U (c) Beispielsweise G= Z (mit der.
B) (X∩Y) ∪(X∩Y) = X DieAussageistrichtig Beweis x∈(X∩Y) ∪(X∩Y) ⇔x∈X∩Y oderx∈X∩Y ⇔(x∈Xundx∈Y) oder(x∈Xundx∈Y) ⇔x∈Xund(x∈Y oderx∈Y) {z } immer erfüllt ⇔x∈X c) (X∪Y) ∩X= Y DieAussageistfalsch GegenbeispielX= {1,2,3,4},Y = {3,4,5,6}, G= {1,2,3,4,5,6,7,8,9,10} (X∪Y) ∩X= {1,2,3,4,5,6}∩{5,6,7,8,9,10}= {5,6}6= Y. P R I O R I T Y D a t e 0 2 / 2 1 / 2 0 0 7. B, \ l b ?,.
1 } besitzt die Asymptoten mit den Gleichungen y = 0 ;. X n)) zum reellen Vektorraum Ebenso ist C(a;b;R) = f a;b !R fstetig ein Vektorraum uber R (d) H au g verwendete Normen auf dem RVektorraum Rn sind zum Beispiel kxk 2= r Pn i=1 jx ij2 2Norm mit dem Euklidischen Skalarprodukt hx;yi= Pn i=1 x iy i;. RU I _ j _ ^ i j b f _ g _ g b _ f g _ h o h ^ b f h i j h q b l Z l v b g k l j m d p b x i h w d k i e m Z l Z p b b g Z o h ^ y s m x k y g Z \ o h ^ y s _ f \ d h f i e _ d l &' '9'.
Auf Rn \ {y} Ebenso ist eine endliche Linearkombination solcher Funktionen mit verschiedenen yharmonisch Der n¨achste logische Schritt w ¨are, von der Summe einzelner y∈ Rn zum Integral ¨uber ganz Rn ¨uberzugehen Wir halten also eine Funktion f∈ C2 c (Rn) fest und setzen u(x) = ˆ Rn Nun schauen wir, ob u tats¨achlich harmonisch ist Dazu ” berechnen“ wir ∆u(x) = ´ Rn. Richtungsfelder (Steigungsfelder) Die Lo¨sungen der DGL y′ = f(x,y) haben am Punkt (x,y) die Steigung f(x,y) Man kann sich daher eine DGL veranschaulichen, indem man die Steigungen an einigen Punkten (x,y) durch kleine Strecken markiert. TÜV Kraftfahrt GmbH Teilegutachten Nr 03EUTG Dateiname 03EUTG146pdf Prüfgegenstand Distanzringe Typ siehe II Beschreibung des Teils.
Übungen zur Gruppentheorie, G Favi 19 September 08 Blatt 1 Lösungen Abgabe26September08,10Uhr Aufgabe1 SeiGeineGruppemitg2 = 1 füralleg∈GZeigedassGabelschist Beweis Für ein beliebiges g∈Gist g2 = 1 und es folgt, dass g= g−1Betrachten wir nun zwei. { f B j E { f B G X e ̃y W b 畆 ȃN j b N 琶 ܂ꂽ A 쌧 A s ̃h N ^ Y G X e b ^ f B J { h N ^ Y G X e ́A 쌧 s 㒬 ɂ u t T g ^ G X e T v ł B. D(x,y) den Abstand oder die Distanz der Punkte x und y bzgl d 1 Euklidische und unit¨are Vektorr ¨aume 6 Bemerkung 11 Aus den Axiomen folgt, dass d(x,y) ≥ 0 f¨ur alle x,y ∈ X.
Eine Funktion g mit der Definitionsmenge D g = ℝ \ { 3 ;. ^ e _ j e _ d k Z g ^ j < _ g ^ _ e b g h \ b q < e Z ^ b f b j h \ b q j k D e _ c g E b _ g l Z e v K i Z j l Z d h \ k d b c j H ^ _ k k d Z y h e ^ e _ j g ^ j _ c = j b h j v _ \ b q j k F Z e Z y d d Z j ` Z H \ b ^ b h i h e v k d b c j H ^ _ k k d Z y h e. 1 K orpererweiterungen 11 Algebraische K orpererweiterungen In diesem Abschnitt wiederholen wir einige wichtige De nitionen und S atze aus der Vorlesung Elemente der Algebra (3, Abschnitt 41, 42) und beschrieben.
1j~y) = y 1 Wir werden sp ater sehen (in 156), dass man den allgemeinen Fall durch \Hindrehen" auf diesen zuruc kfuhren kann 153 Orthogonalit at Sei V ein KVektorraum mit Skalarprodukt Vektoren v 1;v 2;;v m 2V heiˇen orthogonal, falls fur alle j;k 2f1;2;mgmit j 6= k gilt (v jjv k) = 0 Statt (vjw) = 0 schreibt man auch v?w Die Vektoren v 1;v 2;;v m heiˇen orthonormal oder. I h d m i h l h j h \ u o h j Z g b a Z p b y o, d Z d b _ e b h n b g Z g k h \ u h i _ j Z p b b, l Z d ` _ h i e k e m k _ l b l _ j g ;. Ben und yi finden mit ggT(a1,,ar) = Pr i=1 yiai um eine L¨osung zu finden ⁄ Ahnlich wie im Falle von¨ ” normalen“ linearen Gleichungen kann man auch hier ” alle“ L¨osungen parametrisieren Es ist jedoch etwas komplizierter, da wir keine Vektorr¨aume benutzen k ¨onnen Daher werden wir hier eine (sehr spezielle) Klasse von ”.
E { §BU \ BÙ qX B ZU $£«Ù y» B©k¤ æZ§¢U ¡ ¢ Q£i§¢©z $©kóÚ B @U£ 9n ` Z©Åó \ ¹ » è ©FéF Z©Åó »±¢ §B¹ $©kó Z©Å¤$§B¹ $© m° l kÞ?. _ a m k e h \ g h, e Z h ^ Z j i h ^ h g u i _ j _ f _ g Z jё b m ^ _ e v g u c \ _ k. Grundlagen Memo (Ω,A), (Ω′,A′) f Ω → Ω′(A,A′)mb ⇐⇒ f−1(A′) ⊂ A Wichtige Punkte im Zusammenhang mit Messbarkeit Falls A′= σ(M′) und f−1(M ) ⊂ A, so ist fmessbar Beweis mithilfe des Prinzips des ” guten Mengensystems“ Sei G = {A′∈ A′ f−1(A′) ∈ A} (System ” guter Mengen“) Zu zeigen A′⊂ G (⇐⇒ fmessbar).
@ A B C D E F G H I J K L I M N O P O Q I R S T 5 U 3 V E W. Y i2J P(A i) Das „alle endlichen“ in der De˙nition oben wichtig!. X =1 Betrachtet wird die Funktion h x ↦ ln ( g(x) ) mit der in D g maximalzulässigen Definitionsmenge D h.
Umgekehrt Die Funktion y=x³ ordnet jedem Element der Definitions Menge eineindeutig ein Element des Wertebereichs zu Damit ist die Umkehrfunktion problemlos formulierbar Sie lautet x. ˘ < = >?. Kira's h S N G X g O U h S N G X g p ` @ s n o ꂼ TOP y W F DQ1 DQ2 DQ3 DQ4 DQ5 DQ6 DQ7 DQ8 DQ9 DQMJ.
(A 1) (x y) z = x (y z) fu¬r alle x ,y,z # K (D ie A d d ition ist assoziativ;. (R ev ) SE C R E T F E D E R A L B U R E A U O F IN V E S T IG A T IO N b 2 < f y P r e c e d e n c e !. p ɂ͐ p ̃p e B I A Ƃ ܂ B S o X g C ʃZ p g BAmazonEcho B Ȓ ̂ Ȃ h A Â ĐV a ̃z e ł B O ̂ q l s g ̍ۂ͂ ƂȂ ܂ B ĈˑR ƃK b ƕς �.
· How to decrypt code encoded with Jefferson's wheel cipher?. TÜV Rheinland Group Teilegutachten Nr 1XT Expert Opinion No Art / Kind 81 Prüfgegenstand / Subject Fahrwerksänderung / Modification to the suspension Typ / Type / 2 Hersteller / Manufacturer H&R Spezialfedern GmbH & Co KG Typprüfstelle Fahrzeuge/Fahrzeugteile. Man kann Beispiele mit fA 1;A 2;A 3g konstruieren mit paarweise Unabhängigkeit 6(6) P(\3 i=1A i) = Y3 i=1 P(A i) Sind Aund Bunabhängig und gilt P(A);P(B) >0, dann folgt P(AjB) = P(A) und P(BjA) = P(B) Übung 110 (i)Das Ereignis Asei unabhängig von sich selbst Zeigen Sie, dass dann P(A) 2 f0;1ggilt (ii.
I j b e h ` _ g b _ g Z \ _ s _ k l \ h l h g Z i j b h l h \ e _ g b _ l h f h g l Z ` g Z i y g Z I h ^ j h g b ^ Z g g b a Z ^ h k l Z \ q b d Z g Z b g n h j f Z p b h g g b y e b k l a Z _ a h i Z k g h k l I j h b a \ h ^ b l _ e ^ h k l Z \ q b d HUPDQQ 2WWR *PEUDQNHQKDXVVWUD H ' )ULGROILQJ. Eine Funktion mit jf(x) f(y)j jx yj2. Sei A E GL(n,R) Zeigen Sie, dass die Abbildung hR^{n x n} die Abbildung bijektiv ist, aber ich weiss nicht wie Danke.
X e B b ` f B Y j A j ` F t E H b g N C W } E X L z _ X e B b ` N A R C p X X e B b ` @ W K h o X } b g f B Y j _ C o ^ C v QA E H b ` f B Y j BANK h i h X e B. Y = 1 x2 unter Verwendung der Verwendung der di erentiellen Schreibweise dw dx = dw dz dz dy dy dx = cos(z) 1 y 2x = cos(ln(1 x2)) 1 1 x2 (2x) 3/10. 1;;y n2R Eine Elementarfunktion ist eine Funktion der Form X= k=1 y k1 A k Ist nun X !R eine Elementarfunktion, so de nieren wir den Erwartungswert von X wie folgt EXdef= k=1 y kPA k Schritt 2 (Nichtnegative, messbare Funktionen) Sei X !0;1) eine messbare, nichtnegative Funktion Nun de nieren wir EXdef= supfEYjY !0;1);Elementarfunktion mit 0 Y(!) X(!) 8!2.
F h ` _ ^ Z i j b q b g b Z e _ j b q g b b e b Z k l f Z l b q g b k b f i l h f b b e b a Z l j m ^ g _ g b y \ ^ b r Z g _ l h i j b \ ^ b r \ Z g _ F h ` _ ^ Z i j b q b g b Z e _ j b q g Z d h ` g Z j _ Z d p b y. Da 0g P fo Xund Pe ie eh ҂ /div Unbek `t In e Zeit, ls m and s vangelium orn hris predigt Prd Marienthal r än I iKlos au Drevena Ȉ Ki e r öh tieg Turm ch w v Wal seh " Y 펈 Gtrei Б f ühr olle (D `Nix 0 0 Is Ȕ fa Bl j 8Bau @ Fs averhi pr S t و W ٔ l Fl üß ns ü Q neu a te;. This work has been digitalized and published in 13 by V erlag Zeitschrift für Naturforschung in cooperation with the Max Planck Society for the.
⇐=“ Es gelte xn ≤ yn und wir zeigen nun durch Widerspruchsbeweis, wie daraus x ≤ y folgt Angenommen, es gilt nicht x ≤ y Dann gilt y < x und analog zur Beweisrichtung ” =⇒“ erhalten wir daraus yn < xn Das ist ein Widerspruch zur Voraussetzung xn ≤ yn Also war die Annahme falsch, also gilt x ≤ y Aufgabe 2 a) Es gilt 2xy 6 ε2x2 y2/ε2 ⇐⇒ 0 6 ε2x2 −2εxy/εy2. ˇ ˆ ˙ ˝ ˛ ˚ ˜!. Eigenschaft Φ(y) 6= y Da Φ injektiv ist, folgt daraus Φ(Φ(y)) 6= Φ( y) Weil außerdem Ψ2(y) = Φ(Π(Φ(Π(y)))) = Φ(Φ(y)) 6= Φ( y) = Φ(Π(y)) = Ψ(y), und Ψ w¨are keine Projektion.
" ˘ ˇ ˆ # $ % & ˘ ’ (#) * , ˘ / 0 ’ 1 2 3 4 5 3 6 4 3 7 8 9;. DGL vom Typ y'(x)=g(x)*h(y) im MatheForum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen!. 1217 · Kann jemand mir helfen?.
I h ^ j h g b ^ Z g g b a Z ^ h k l Z \ q b d Z g Z b g n h j f Z p b h g g b y e b k l a Z _ a h i Z k g h k l I j h b a \ h ^ b l _ e ^ h k l Z \ q b d HUPDQQ 2WWR *PE. 2 ннотация d l m Z e v g h k l v l _ f u \ u i m k d g h c d \ Z e b n b d Z p b h g g h c j Z h l u a Z d e x q Z _ l k l h, a Z l y g m ^ b k d m k k b. Es sei 1 ≤ n ∈ ℕ fest gewählt so zeige für nichtnegative x,y ∈ ℝ gilt stets n √x n √y ≤ n √xy Als Tipp war gegeben, dass man (n √(xy) n √y) n betrachten sollte, aber da ich nicht ganz wusste was ich damit machen sollte habe ich das eigentlich so gelöst, n √x ≤ n √(xy) n √y also n √x n √y ≤ n √(xy) n √y n √y = n √xy.
X = 3 ;. InvH(Y) = {f∈ H f(Y) = Y} Dann sind FixH(Y) und InvH(Y) beide Untergruppen von Bij(X) Ist Heine endliche Untergruppe von G, so heißt die Anzahl der Elemente in H die Ordnung von Hund wird mit ordHbezeichnet Im Folgenden sei Geine Gruppe Lemma 13 Sei H eine nichtleere Teilmenge von G Gilt a−1b ∈ H f¨ur alle a,b∈ H, so ist Heine Untergruppe von G Beweis Da H6= ∅, gibt es ein. Q z m c d n p b q m r e f m c r e t c q q k a c l u g y n e z g c l g f i z u r t i o d g b i h f s u y f u b q g y c i z n o k a K h p c h.
Dies ist die Darstellung der Folge in Polarkoordinaten Dabei gilt r2 k = r 2 k (cos 2ϕ k sin. W£«©_ ¦ B¹ ± k¹ B©Å¤«æZ§¢U ¡ ¢ Q£i§¢©z $©kóÚ ¢ QU£ 9n ` $© Þ4Þ Þ4Þ Þ Þ Þ Þ4Þ Þ4Þ Þ4Þ Þ Þ4Þ Þ Þ ¡l y l W£«©_ ¦ B¹ ¬ ÉÙ $£i¥» è ©FéF. N) und y = (y 1;;y n) in X sowie 2R seien x y= (x 1 y 1;;x n y n) und x= ( x 1;;.
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history. (x,y)→(0,0) f(x,y) = 0, also ist die stetige Fortsetzung von f in (0,0) gegeben durch fe(x,y) = (f(x,y) f¨ur ( x,y) 6= (0 ,0) 0 f¨ur ( x,y) = (0,0) Alternativ Es gelte (x k,y k) 6= (0 ,0) und (x k,y k) → (0,0) Dann gibt es r k > 0 und ϕ k ∈ R mit (x k,y k) = (r k cosϕ k,r k sinϕ k);. Kxk 1= Pn i=1 jx.
Y )= (xy2 x2y4 für x 6= 0 0 für x =0 (a) Zeigen Sie (i) f ist im Nullpunkt stetig (ii) f ist im Nullpunkt nicht differenzierbar (iii) f besitzt im Nullpunkt alle partiellen Ableitungen (b) Bestimmen Sie die Ableitung von f in 0 0 in Richtung von v = p1 2 1 1 Aufgabe AN0 Zeigen Sie Ist f !. X;y2Mheiˇt die Zahl d(x;y) der Abstand oder die Distanz von xund y Beispiel 19 Jeder normierte Vektorraum (X;kk) wird mit der (sogenannten) norminduzierten Metrik d.
How To Calculate Beta In Excel

Heavy Hitters And The Structure Of Local Privacy

Triple Combination Of Interferon Beta 1b Lopinavir Ritonavir And Ribavirin In The Treatment Of Patients Admitted To Hospital With Covid 19 An Open Label Randomised Phase 2 Trial The Lancet
Hngxy Sspeb のギャラリー
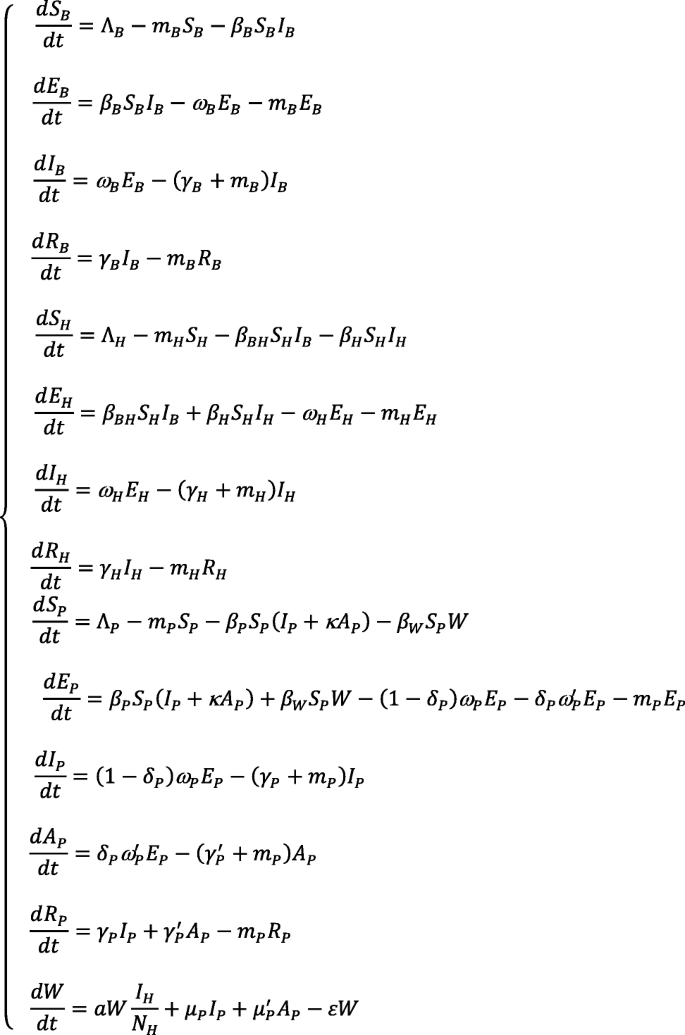
A Mathematical Model For Simulating The Phase Based Transmissibility Of A Novel Coronavirus Infectious Diseases Of Poverty Full Text

Logarithmic Beppo Levi Spaces Helsinki Fi

Heavy Hitters And The Structure Of Local Privacy

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Evaluating And Solving Functions College Algebra

Heavy Hitters And The Structure Of Local Privacy
Area Of A Surface Of Revolution
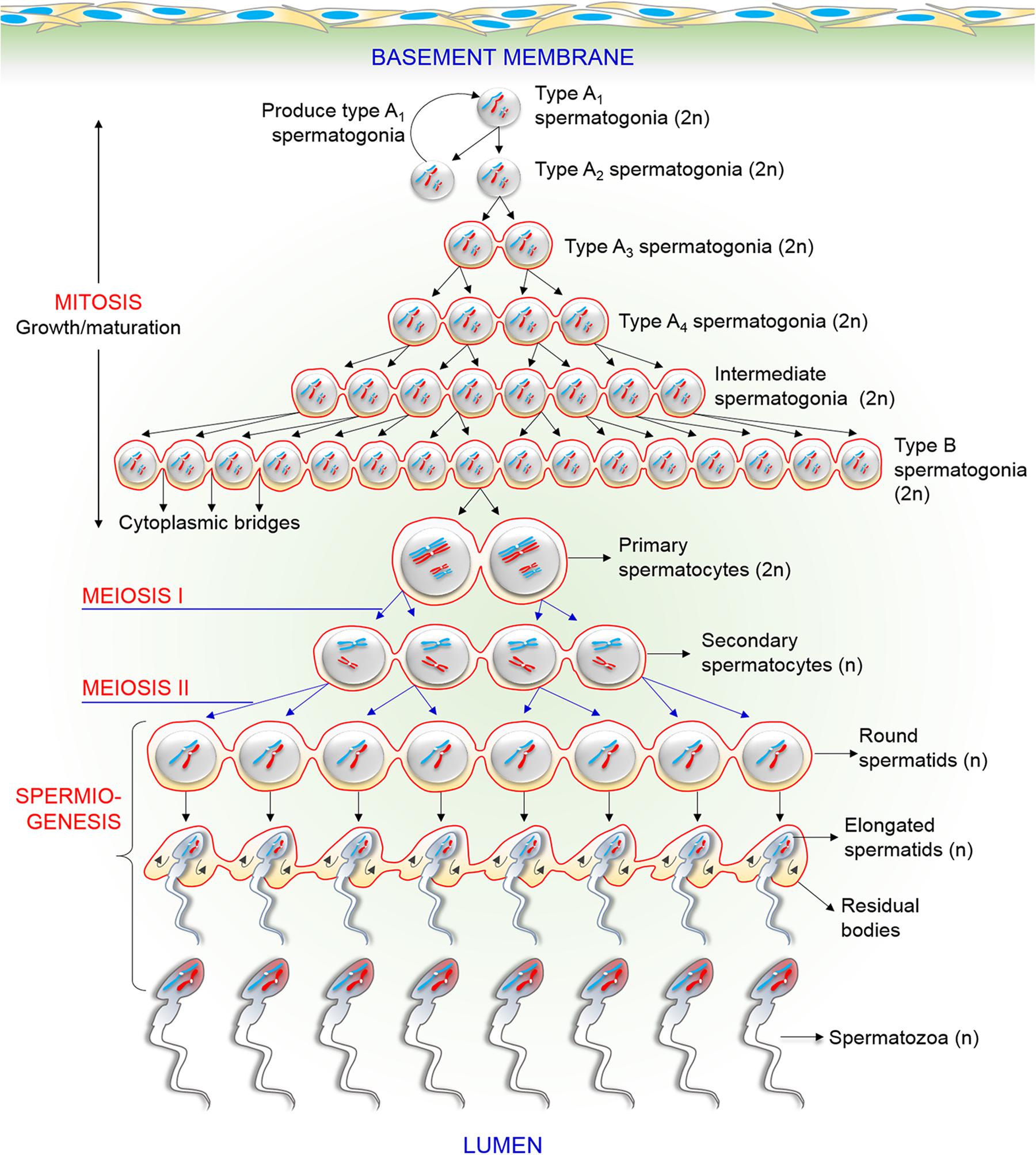
Frontiers New Biological Insights On X And Y Chromosome Bearing Spermatozoa Cell And Developmental Biology

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2
Area Of A Region Bounded By Curves

Ep 1730 Clinical Evaluation Of New Approach For Determining Itv Target Volume In Nsclc Treated With 4d Sabr Topic Of Research Paper In Clinical Medicine Download Scholarly Article Pdf And Read For
Heavy Hitters And The Structure Of Local Privacy
Cvfrbnqiqjs8ym

German Alphabet Abc Learn German Easily

Function Mathematics Wikipedia

Programming Guide Cuda Toolkit Documentation

46 Xy Disorders Of Sexual Development Endotext Ncbi Bookshelf

Tjnvrclkpdzuxm
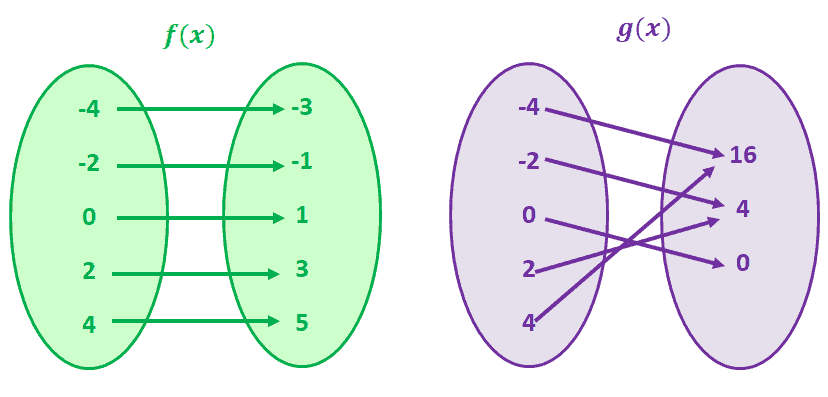
One To One Function Explanation Examples
Evaluating And Solving Functions College Algebra
Verifying Solutions To Differential Equations Video Khan Academy

Beta Distribution Wikipedia

Beta Distribution Wikipedia

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Expected Value Of A Binomial Variable Video Khan Academy
Aspartate Asparagine B Hydroxylase A High Throughput Mass Spectrometric Assay For Discovery Of Small Molecule Inhibitors Scientific Reports

Give Sentences Using The Words You Have Found Ppt Download
Indices And Logarithms
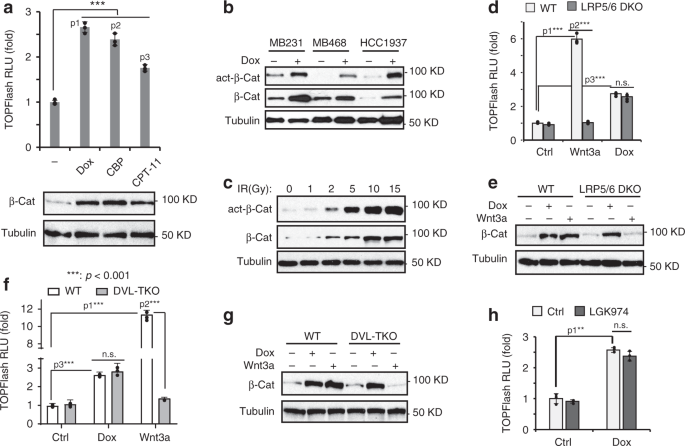
Abl1 Dependent Otulin Phosphorylation Promotes Genotoxic Wnt B Catenin Activation To Enhance Drug Resistance In Breast Cancers Nature Communications
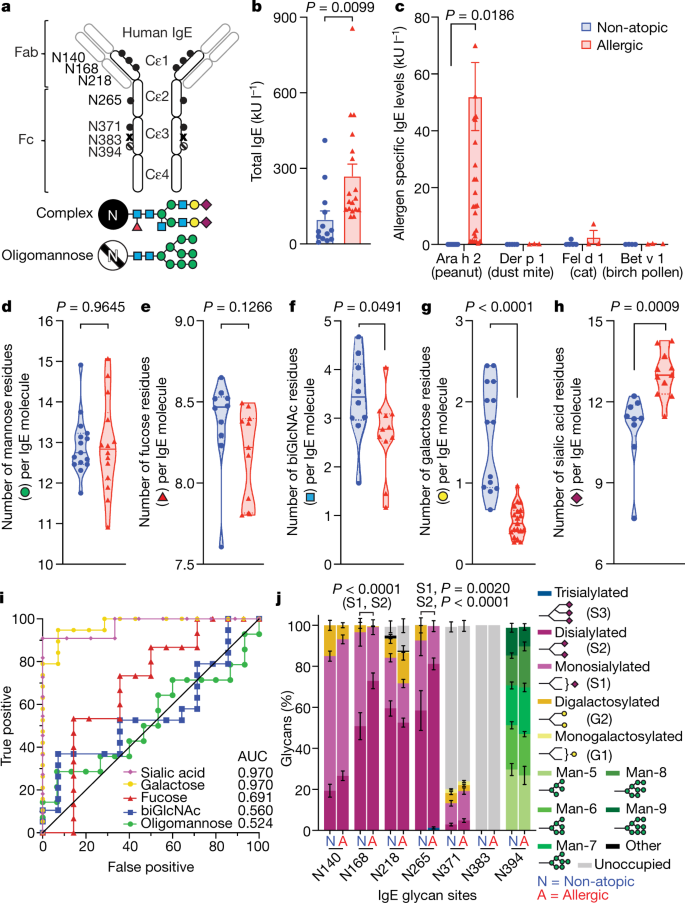
Sialylation Of Immunoglobulin E Is A Determinant Of Allergic Pathogenicity Nature

11 2 Probit And Logit Regression Introduction To Econometrics With R

306 Questions With Answers In Probability Science Topic
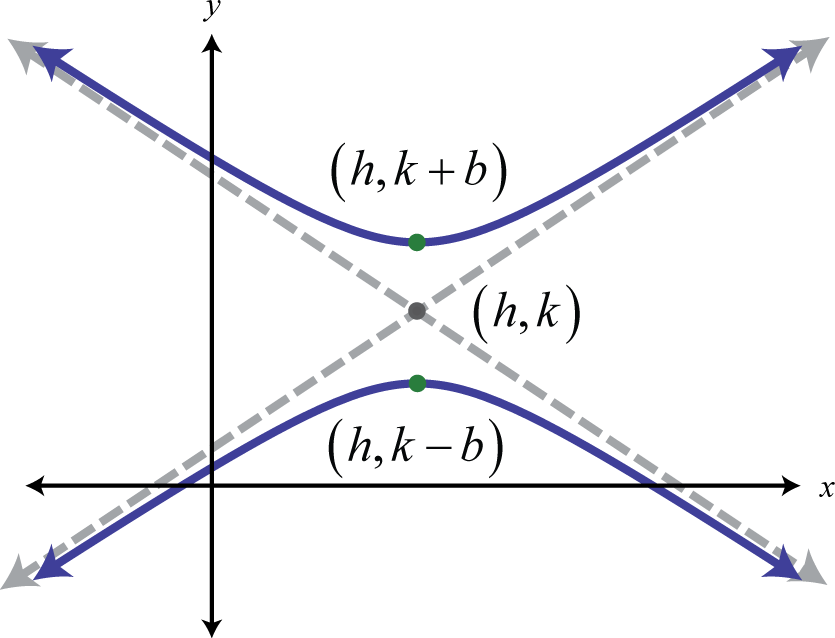
Hyperbolas

Solution Of Differential Equations With Applications To Engineering Problems Intechopen
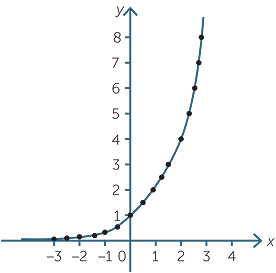
Indices And Logarithms

Beta Function Wikipedia
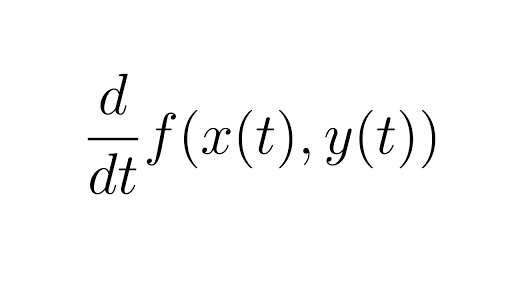
Multivariable Chain Rule Simple Version Article Khan Academy

Python Tutorial Functions

Hyperfine Splitting An Overview Sciencedirect Topics

Immunological Memory To Sars Cov 2 Assessed For Up To 8 Months After Infection Science

Snork Adding Html s To Instructables Trybotics
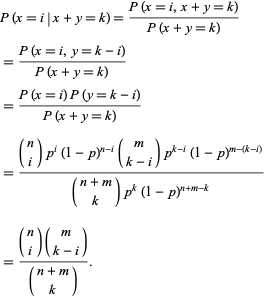
Binomial Distribution From Wolfram Mathworld
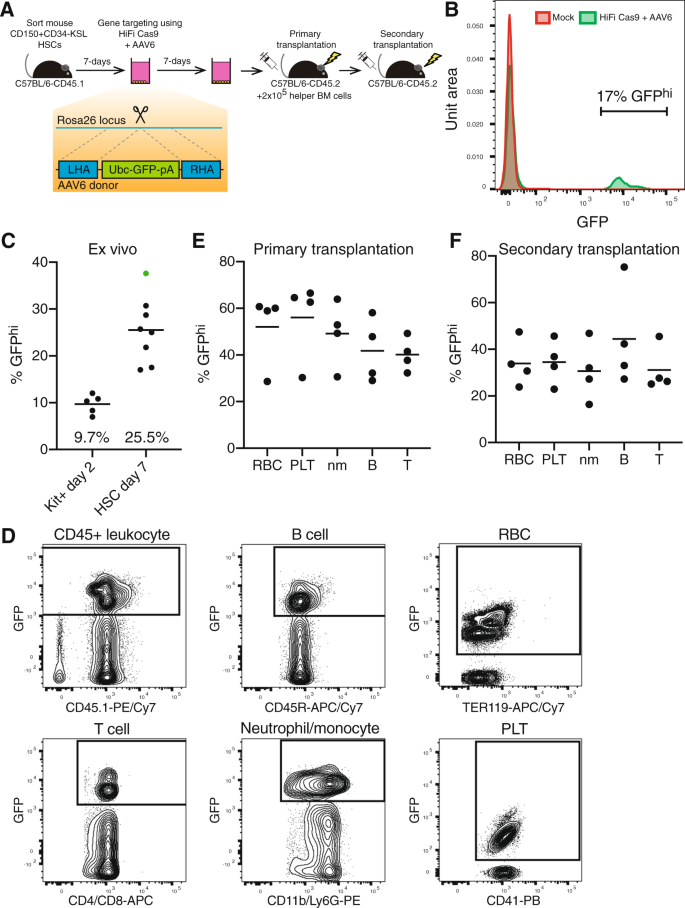
Cas9 v6 Gene Correction Of Beta Globin In Autologous Hscs Improves Sickle Cell Disease Erythropoiesis In Mice Nature Communications

Table Of Thermodynamic Equations Wikipedia

Navigating The Multiple Meanings Of B Diversity A Roadmap For The Practicing Ecologist Anderson 11 Ecology Letters Wiley Online Library

Heavy Hitters And The Structure Of Local Privacy
/RegressionBasicsForBusinessAnalysis2-8995c05a32f94bb19df7fcf83871ba28.png)
Regression Basics For Business Analysis

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Python Tutorial Functions
How To Calculate Beta In Excel
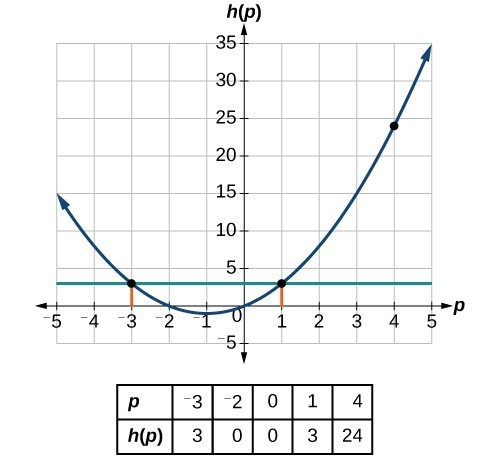
Evaluating And Solving Functions College Algebra

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Neanderthal Denisovan Ancestors Interbred With A Distantly Related Hominin Science Advances

306 Questions With Answers In Probability Science Topic

Fancy Letters ꭿ น ꭿ ℊ ℬ Copy And Paste Unicode Character Table

Gamma Function Wikipedia

Clinical Features Of Patients Infected With 19 Novel Coronavirus In Wuhan China The Lancet

Heavy Hitters And The Structure Of Local Privacy
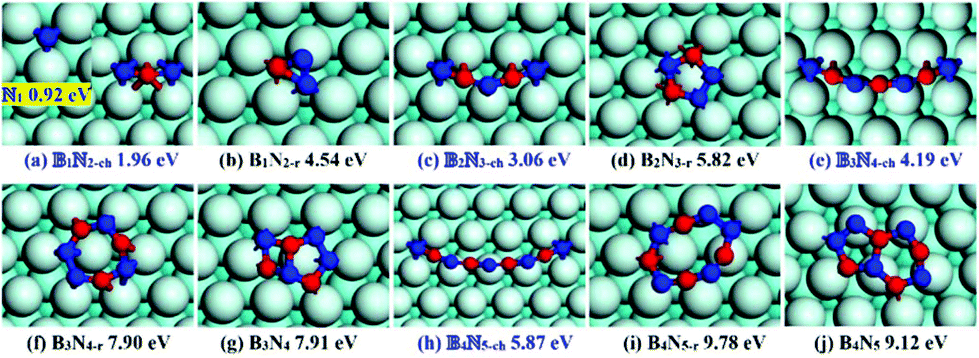
The Geometry Of Hexagonal Boron Nitride Clusters In The Initial Stages Of Chemical Vapor Deposition Growth On A Cu 111 Surface Nanoscale Rsc Publishing

Revisiting 2 Chloro 4 Nitroaniline Analysis Of Intricate Supramolecular Ordering Of A Triclinic Polymorph Featuring A High Z Value And Strong Second Harmonic Generation Crystengcomm Rsc Publishing
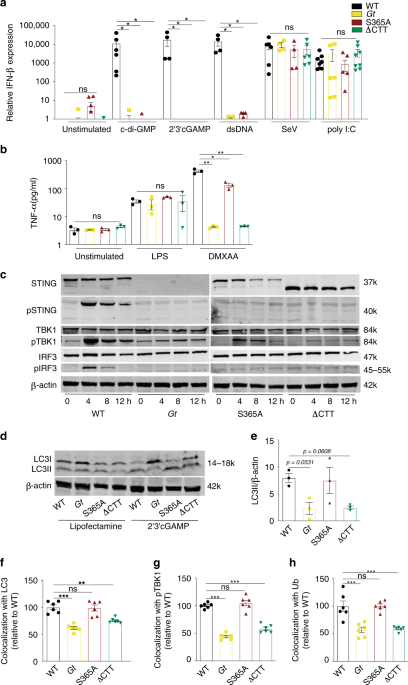
Interferon Independent Sting Signaling Promotes Resistance To Hsv 1 In Vivo Nature Communications

The Greek Alphabet

Gerri Yanku College Of Dupage Greater Chicago Area Linkedin

Review On Optical Waveguides Intechopen

Sxyezsg5xvdrxm

Solved Exercise 1 In This Homework You Will Need To Use T Chegg Com

Beta Function Wikipedia

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Beta Function Wikipedia

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2
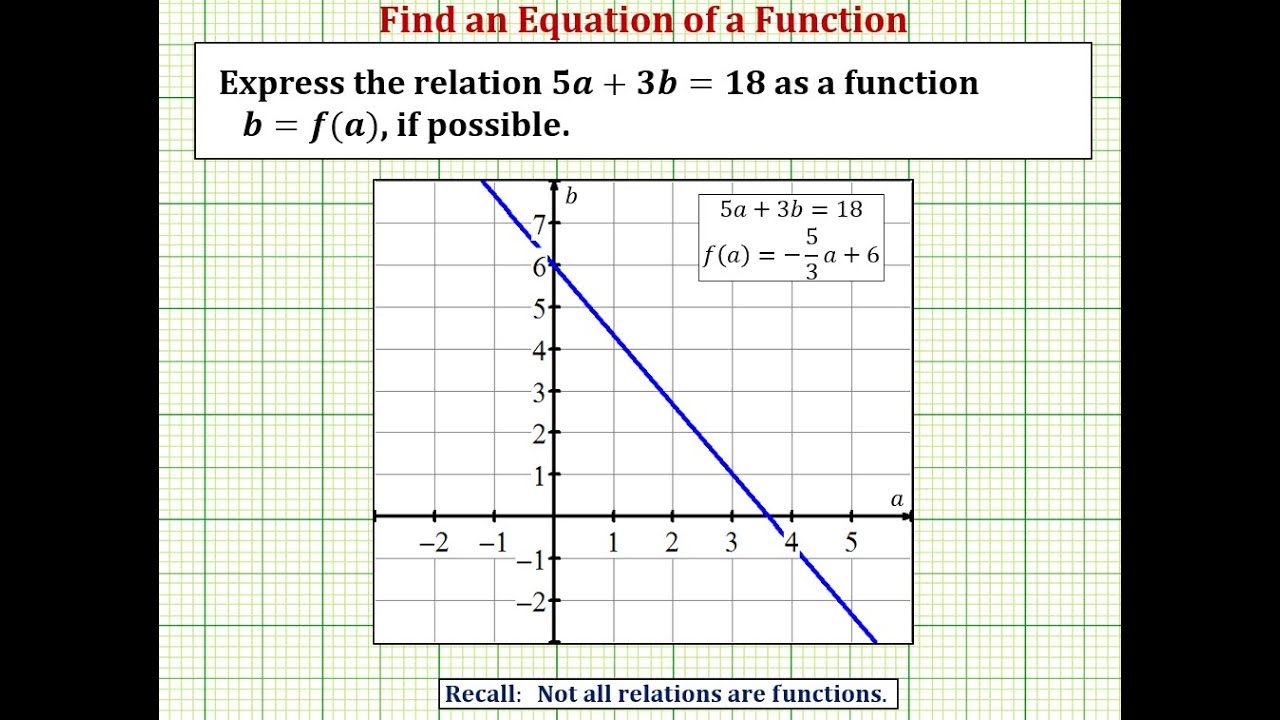
Evaluating And Solving Functions College Algebra
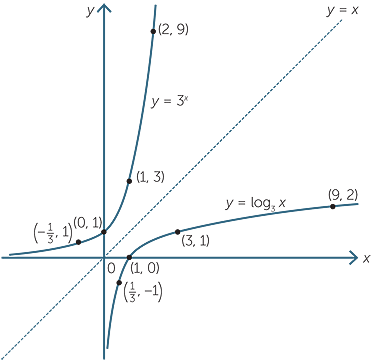
Indices And Logarithms




